How Gradient Boosting Does Gradient Descent
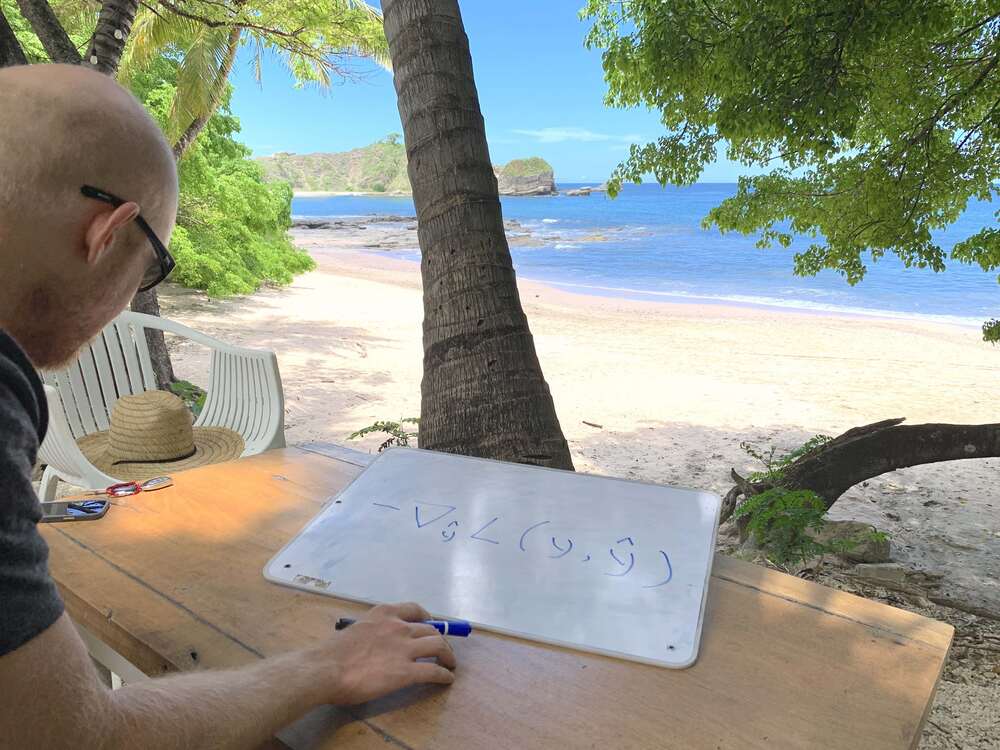
In the last two posts, we learned the basics of gradient boosting machines and the gradient descent algorithm. But we still haven’t explicitly addressed what puts the “gradient” in gradient boosting. It turns out that gradient boosting models are using a sort of gradient descent to minimize their loss function; according to Friedman’s classic paper, they’re doing gradient descent in “function space”. If you’re like me, and this is your first encounter with this idea, then the phrase “gradient descent in function space” is going to sound a little, ahem, mysterious. No worries, friends; we’re about to make sense of it all.
Understanding the underlying mechanics of gradient boosting as a form of gradient descent will empower us to train our models with custom loss functions. This opens up many interesting possibilities including doing not only regression and classification, but also predicting quantiles, prediction intervals, and even the conditional probability distribution of the response variable.
Generalized intuition for gradient boosting
In my earlier post on building a gradient boosting model from scratch, we established the intuition for how gradient boosting works in a regression problem. In this post we’re going to generalize the ideas we encountered in the regression context, so check out the earlier post if you’re not already familiar with gradient boosting for regression. In the following sections we’ll build up the intuition for gradient boosting in general terms, and then we’ll be able to state the gradient boosting algorithm in a form that can fit models to customized loss functions.
The loss function
You recall that we measure how well a model fits data by using a loss function that yields small values when a model fits well. “Training” essentially means finding the model that minimizes our loss function. A loss function takes the correct target values and the predicted target values, and it returns a scalar loss score. For example, in the last post on gradient descent we used a mean squared error (MSE) loss
\[L(\mathbf{y}, \hat{\mathbf{y}}) = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 \]
where we express the correct targets and predicted values as the vector arguments \(\mathbf{y}=[y_1,y_2,\dots,y_n]\) and \(\hat{\mathbf{y}}=[\hat{y}_1,\hat{y}_2,\dots,\hat{y}_n]\) respectively.
Which way to nudge a prediction to get a better model
Now, let’s say we have a model \(F(\mathbf{X})=\mathbf{\hat{y}}\) that we want to improve. One approach is that we could figure out whether each prediction \(\hat{y}_i\) needed to be higher or lower to get a better loss score. We could then nudge each prediction in the right direction, thereby decreasing our model’s loss score.
To figure out whether we should increase or decrease a particular prediction \(\hat{y}_i\) (and by how much), we can compute the partial derivative of the loss function with respect to that prediction. Recall the partial derivative just tells us the rate of change in a function when we change one of its arguments. Since we want to make the loss \(L(\mathbf{y},\mathbf{\hat{y}})\) decrease, we can use the negative partial derivative of the loss function with respect to a given prediction to help us choose the right nudge for that prediction.
\[ \text{nudge for } \hat{y}_i = -\frac{\partial L(\mathbf{y},\mathbf{\hat{y}})}{\partial \hat{y}_i}\]
Sometimes it can get a little intense when there are partial derivatives flying around, but it doesn’t have to be that way. Remember that in practice \(-\frac{\partial L(\mathbf{y},\mathbf{\hat{y}})}{\partial \hat{y}_i}\) is just an expression that evaluates to a number like 2.7 or -0.5, and here it’s telling us how to nudge \(\hat{y}_i\) to decrease our loss score.
The intuition is that if \(\frac{\partial L(\mathbf{y},\mathbf{\hat{y}})}{\partial \hat{y}_i}\) is negative, then increasing the prediction \(\hat{y}_i\) will make the loss decrease. We then notice that the negative of the partial derivative tells us whether to increase or decrease \(\hat{y}_i\). For example, if \(-\frac{\partial L(\mathbf{y},\mathbf{\hat{y}})}{\partial \hat{y}_i}\) is positive, then increasing the prediction \(\hat{y}_i\) will make the loss decrease; whereas if \(-\frac{\partial L(\mathbf{y},\mathbf{\hat{y}})}{\partial \hat{y}_i}\) is negative, then decreasing the prediction \(\hat{y}_i\) will make the loss decrease.
Since we’ll want to find the right nudge for each of the \(\hat{y}_i\)’s, we can use the negative gradient of the loss function \(L(\mathbf{y},\mathbf{\hat{y}})\) with respect to the vector argument \(\hat{\mathbf{y}}\) to get the vector of all the partial derivatives. Let’s call this vector of desired nudge values \(\mathbf{r}\).
\[\mathbf{r} = -\nabla_{\hat{\mathbf{y}}} L(\mathbf{y}, \hat{\mathbf{y}}) = \left [ -\frac{\partial L(\mathbf{y},\mathbf{\hat{y}})}{\partial \hat{y}_1}, -\frac{\partial L(\mathbf{y},\mathbf{\hat{y}})}{\partial \hat{y}_2}, \cdots, -\frac{\partial L(\mathbf{y},\mathbf{\hat{y}})}{\partial \hat{y}_n}\right ]\]
Nudging predictions in the right direction
Great, now that we know we should nudge each prediction in the direction of the negative partial derivative of the loss with respect to that prediction, we need to figure out how to do the actual nudging. Remember that we already have an initial model \(F(\mathbf{X})=\mathbf{\hat{y}}\).
At this point we might be tempted to simply add the vector of nudge values to our predictions to get better predictions.
\[\text{we might be tempted to try } \mathbf{\hat{y}}_{\text{new}} = \mathbf{\hat{y}} + \mathbf{r}\]
Sure, based on our reasoning in the previous section, plugging the vector of nudged predictions into the loss function would yield a lower loss score.
\[ L(\mathbf{y},\mathbf{\hat{y}} + \mathbf{r}) \le L(\mathbf{y},\mathbf{\hat{y}})\]
The problem is that this will only work for in-sample data, because we only know the nudge values for the cases which are present in the training dataset. In order for our model to generalize to unseen test data, we need a way to get the nudge values for new observations of the independent variables. So how can we do that?
Well what if we fit another model \(h(\mathbf{X})\) that used our same features \(\mathbf{X}\) to predict our desired nudge values \(\mathbf{r}\), and then we added that new model to our original model \(F(\mathbf{X})\). For a given prediction the nudge model \(h(\mathbf{X})\) would essentially return an approximation of the desired nudge, so adding it would push the prediction in the right direction to decrease the loss function. Furthermore, the nudge model can return predictions of the nudges for out-of-sample cases which are not present in the training dataset. Since both the initial model \(F(\mathbf{X})\) and the nudge model \(h(\mathbf{X})\) are functions of our features \(\mathbf{X}\), we can add the two functions to get an updated model that can generalize beyond the training data.
\[F_{\text{new}} (\mathbf{X}) = F(\mathbf{X}) + h(\mathbf{X})\]
A generalized gradient boosting algorithm
Ok, let’s put these pieces of intuition together to create a more general gradient boosting algorithm recipe.
We begin with training data \((\mathbf{y}, \mathbf{X})\) where \(\mathbf{y}\) is a length-\(n\) vector of target values, and \(\mathbf{X}\) is an \(n \times p\) matrix with \(n\) observations of \(p\) features. We also have a differentiable loss function \(L(\mathbf{y}, \mathbf{\hat{y}})\), a “learning rate” hyperparameter \(\eta\), and a fixed number of model iterations \(M\).
We create an initial model \(F_0(\mathbf{X})\) that predicts a constant value. We choose the constant value that would give the best loss score.
\[F_0(\mathbf{X}) = \underset{c}{\operatorname{argmin}} L(\mathbf{y}, c)\]
Then we iteratively update the initial model with \(M\) nudge models.
For \(m\) in 0 to \(M-1\):
- Compute current composite model predictions \(\mathbf{\hat{y}}_{m} = F_{m}(\mathbf{X})\).
- Compute the desired nudge values given by the negative gradient of the loss function with respect to each prediction \(\mathbf{r}_m = - \nabla_{\mathbf{\hat{y}}_m} L (\mathbf{y}, \mathbf{\hat{y}}_m)\).
- Fit a weak model (e.g. shallow decision tree) \(h_{m}(\mathbf{X})\) that predicts the nudge values \(\mathbf{r}_{m}\) using features \(\mathbf{X}\).
- Update the composite model.
\[F_{m+1}(\mathbf{X}) = F_{m}(\mathbf{X}) + \eta h_{m}(\mathbf{X})\]
After \(M\) iterations, we are left with the final composite model \(F_M(\mathbf{X})\).
Wait, in what sense is this doing gradient descent?
In my previous post, we learned how to use gradient descent to iteratively update model parameters to find a model that minimizes the loss function. We could write the update rule as
\[ \mathbf{\theta}_{t+1} = \mathbf{\theta}_{t} + \eta ( - \nabla_{\mathbf{\theta}} L(\mathbf{y}, \mathbf{\hat{y}}_{\mathbf{\theta}_{t}}) ) \]
where the predictions \(\mathbf{\hat{y}}\) depend on the model parameters \(\mathbf{\theta}\), and we’re trying to find the value of the parameter vector \(\mathbf{\theta}\) that minimizes the loss function \(L(\mathbf{y}, \mathbf{\hat{y}}_{\mathbf{\theta}_{t}})\), so we nudge the vector \(\mathbf{\theta}_t\) by the negative gradient of \(L(\mathbf{y}, \mathbf{\hat{y}}_{\mathbf{\theta}_{t}})\) with respect to \(\mathbf{\theta}_t\). Compare that with the boosting model update rule we obtained in the previous section.
\[F_{m+1}(\mathbf{X}) = F_{m}(\mathbf{X}) + \eta h_{m}(\mathbf{X})\]
where \(h_{m}(\mathbf{X}) \approx - \nabla_{\mathbf{\hat{y}}_m} L (\mathbf{y}, \mathbf{\hat{y}}_m)\).
If we replace \(F(\mathbf{X})\) with its prediction vector \(\mathbf{\hat{y}}\), and we replace the nudge model \(h(\mathbf{X})\) with the negative gradient of the loss function (which it approximates), the likeness to the parameter gradient descent update rule becomes more obvious.
\[\mathbf{\hat{y}}_{m+1} \approx \mathbf{\hat{y}}_m + \eta (- \nabla_{\mathbf{\hat{y}}_m} L (\mathbf{y}, \mathbf{\hat{y}}_m))\]
Indeed, gradient boosting is performing gradient descent to obtain a good model by minimizing a loss function. But there are a couple of key differences between gradient boosting and the parameter gradient descent that we discussed in the previous post.
Gradient boosting versus parameter gradient descent
The generic gradient boosting algorithm outlined above implies two key differences from parameter gradient descent.
- Instead of nudging parameters, we nudge each individual prediction, thus instead of taking the gradient of loss with respect to the parameters, we take the gradient with respect to the predictions.
- Instead of directly adding the negative gradient to our current parameter values, we create a functional approximation of the negative gradient and add that to our model. Our functional approximation is just a crappy model that tries to use the model features to predict the negative gradient of the loss with respect to our current model predictions.
The true genius of the gradient boosting algorithm is in chasing the negative gradient of the loss with crappy models, rather than using it to directly update our predictions. If we just directly added the negative gradient of the loss to our predictions, and plugged them into the loss function we could get a lower loss score, but our updated model would be useless since it couldn’t make predictions on new out-of-sample data. Instead we train a crappy model to predict the negative gradient of the loss with respect to the current model predictions, thus we can iteratively update our composite model by adding these crappy models to it.
Gradient boosting is gradient descent in function space, a.k.a. prediction space
Let’s address the statement in Friedman’s classic paper that gradient boosting is doing gradient descent in function space. Again we’ll use parameter gradient descent as a basis for comparison.
In parameter gradient descent, we have a vector of parameter values which, when plugged into the loss function, return some loss score. At each step of gradient descent, we compute the negative gradient of the loss function with respect to each parameter; that tells us which way to nudge each parameter value to achieve a lower loss score. We then add this vector of parameter nudge values to our previous parameter vector to get the new parameter vector. We could view this sequence of successive parameter vectors as a trajectory passing through parameter space, the space spanned by all possible parameter values. Therefore parameter gradient descent operates in parameter space.
In contrast, when we do gradient boosting, at each step we have a model, a.k.a. a function, that maps feature values to predictions. Given our training dataset, this model yields predictions which can be plugged into our loss function to get a loss score. At each boosting iteration, we compute the negative gradient of the loss with respect to each of the predictions; that tells us which way to nudge each prediction to achieve a lower loss score. We then create a function (a crappy model) that takes feature values and returns an approximation of the corresponding prediction’s nudge value. We then add this crappy model (a function) to our current composite model (also a function) to get the new composite model (you guessed it; also a function). And so by analogy with parameter vectors in parameter space, we can view this sequence of successive model functions as a trajectory passing through function space, the space spanned by all possible functions that map feature values to predictions. Therefore, gradient boosting does gradient descent in function space.
If this talk about function space still feels a little abstract, you could just use the same substitution trick we used above and swap the model \(F(\mathbf{X})\) for its predictions \(\mathbf{\hat{y}}\) which is just a vector of numbers. The target values for our nudge models are given by the negative gradient of the loss with respect to this prediction vector. From here, we can see that each time we add a new nudge model to our composite model, we get a new prediction vector. We can view this sequence of successive prediction vectors as a trajectory passing through prediction space, the space spanned by all possible prediction vector values. Therefore we can also say that gradient boosting does gradient descent in prediction space.
So why did we fit the crappy models to the residuals in our regression GBM?
In my first post on [gradient boosting machines](/gradient-boosting-machine-from-scratch, in the interest of simplicity I left one key aspect of the problem unaddressed, that is, what loss function were we using to train that GBM? It turns out that because of the way we built our GBM, without knowing it we were actually using a mean squared error (MSE) loss function.
\[L(\mathbf{y}, \hat{\mathbf{y}}) = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 \]
If the GBM was using gradient descent to find a \(\hat{\mathbf{y}}\) vector that minimized this loss function, then at each iteration it would have to nudge the current \(\hat{\mathbf{y}}\) by the negative gradient of the loss function with respect to \(\hat{\mathbf{y}}\), i.e. \(-\nabla_{\hat{\mathbf{y}}} L(\mathbf{y}, \hat{\mathbf{y}})\). Since our loss function takes a length \(n\) vector of predictions \(\hat{\mathbf{y}}\) as input, the gradient will be a length-\(n\) vector of partial derivatives with respect to each of the predictions \(\hat{y}_i\). Let’s start by taking the negative partial derivative with respect to a particular prediction \(\hat{y}_j\).
\[ \begin{array}{rcl} -\frac{\partial}{\partial \hat{y}_j} L(\mathbf{y}, \mathbf{\hat{y}}) & = & -\frac{\partial}{\partial \hat{y}_j} \left ( \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 \right ) \\ & = & -\frac{\partial}{\partial \hat{y}_j} \left ( \frac{1}{n} (y_j - \hat{y}_j)^2 \right ) \\ & = & -\frac{1}{n} (2)(y_j - \hat{y}_j) \frac{\partial}{\partial \hat{y}_j} (y_j - \hat{y}_j) \\ & = & \frac{2}{n} (y_j - \hat{y}_j) \\ \end{array} \]
It turns out that the negative partial derivative of the MSE loss function with respect to a particular prediction \(\hat{y}_i\) is proportional to the residual \(y_i - \hat{y}_i\)! This is a pretty intuitive result, because if we nudge a prediction by it’s residual, we’ll end up with the correct target value.
We can go ahead and write the nudge vector as
\[\mathbf{r} = -\nabla_{\hat{\mathbf{y}}} L(\mathbf{y}, \hat{\mathbf{y}}) = \frac{2}{n}(\mathbf{y} - \hat{\mathbf{y}})\]
which is proportional to the residual vector \(\mathbf{y} - \hat{\mathbf{y}}\). This means that when we use the mean squared error loss function, our nudge values are given by the current model residuals, and therefore each new crappy model targets the previous model’s residuals.
And this result brings us full circle, back to our original intuition from the first GBM post about chasing residuals with crappy models. Now we see that intuitive idea is just a special case of the more general and, dare I say, even more beautiful idea of chasing the negative gradient of the loss function with crappy models.
Key Takeaways
We covered a lot of conceptual ground in this post, so let’s recap the key ideas.
- Gradient boosting can use gradient descent to minimize any differentiable loss function in service of creating a good final model.
- There are two key differences between gradient boosting and parameter gradient descent:
- In gradient boosting, we nudge prediction values rather than parameter values, so to find the desired nudge values, we take the negative gradient of the loss function with respect to the predictions.
- In gradient boosting, we nudge our predictions by adding a crappy model that approximates the nudge values, rather than adding the nudge values directly to the predictions.
- Gradient boosting does gradient descent in function space. But since the model predictions are just numeric vectors, and since we take the gradient of the loss function with respect to the prediction vector, it’s also valid and probably easier to think of gradient boosting as gradient descent in prediction space.
- We saw that iteratively fitting crappy models to the previous model residuals, as we did in the regression GBM from scratch post, is just a special case of fitting crappy models to the negative gradient of the loss function (in this case the mean squared error loss).
Wrapping Up
Phew, there it is, how gradient boosting models do gradient descent in function space. Understanding how the general form of gradient boosting works opens up the possibility for us to use any differentiable loss function for model training. That is pretty exciting because it means that we can get a lot of mileage out of this one class of learning algorithms. Stay tuned for more on some of the awesome things we can do with these ideas in future posts!
There are a couple of resources I found to be super helpful while researching the content in this post. Definitely check them out if you want to read more about gradient boosting and gradient descent.
How to explain gradient boosting by Terence Parr and Jeremy Howard
Understanding Gradient Boosting as Gradient Descent by Nicolas Hug